728x90
반응형
SMALL
분석기법
1. 회귀분석 (Regression)
1.1 회귀분석
| 항목 | 설명 |
| 정의 | 독립변수(X)가 종속변수(Y)에 어떤 영향을 미치는지 분석하는 통계 기법 |
| 독립변수(X) | 원인(예측 변수) |
| 종속변수(Y) | 결과(반응 변수) |
| 잔차 | 실제값과 예측값의 차이 (오차 = yi−yi^y_i - \hat{y_i}) |
- 회귀계수 추정
- 목적: 잔차 제곱합(SSE, Sum of Squared Errors)을 최소화하는 선형 회귀식 도출
- β0: 절편
- β1: 회귀계수
- ε: 오차
Y=β0+β1X+ε
- 결정계수 (R -Squared, R²)
- 결정력이라고도 불리는 결정계수는 회귀분석의 성능 평가 척도 중 하나
- 독립변수가 종속변수를 얼마나 잘 설명하는 지 나타냄
- 상관계수를 제곱한 값
- 0 ≤ R² ≤ 1 , 상관계수가 높을 수록 1에 가까워지고 이는 설명력이 높음
- R² 값이 0.3이라면, 모델이 약 30%의 설명력을 가진다고 해석
- 결정계수는 독립변수가 많을수록 값이 커지기 때문에, 독립변수가 2개 이상일 경우 조정된 결정계수를 사용
- SST = SSR + SSE

1.2 선형회귀 분석의 4대 가정
| 가정 | 가정 |
| 선형성 | X와 Y의 관계가 선형이어야 함 |
| 등분산성 | 잔차의 분산이 일정해야 함 (Homoscedasticity) |
| 정규성 | 잔차가 정규분포를 따라야 함 |
| 독립성 | 독립변수들 간 다중공선성이 없어야 함(상관성을 줄여야 함) |
✅ 다중공선성 검출 지표:
- VIF(분산 팽창 계수)
- VIF > 10 → 다중공선성 존재
1.3 회귀분석 종류
| 종류 | 설명 |
| 단순회귀 | 독립변수 1개, 종속변수 1개 |
| 다중회귀 | 독립변수 2개 이상 |
| 다항회귀 | 독립변수와 종속변수 관계가 비선형 (2차 이상) |
| 릿지 회귀 | L2 정규화 사용 → 계수 크기 억제 (다중공선성 대응) |
| 라쏘 회귀 | L1 정규화 사용 → 불필요 변수 계수 0으로 만듦 (변수 선택 기능 있음) |
| 교호작용 회귀 | X₁ * X₂처럼 두 변수 간 상호작용을 포함한 회귀식 |
1.4 회귀 모형의 구축 절차
- 문제 정의 및 변수 설정
- Y (종속변수), X (독립변수) 정의
- 회귀계수 추정
- 최소제곱법(OLS) 등으로 β 추정
- 계수 유의성 검정
- t-검정 활용 (각 β가 0인지 확인)
- 모형 전체 유의성 검정
- F-검정 활용 (모형이 통계적으로 유의한지)
1.5 회귀 모형의 변수 선택 방법
| 기법 | 설명 |
| 전진선택법 | 하나씩 변수를 추가하며 성능 개선 여부 확인 |
| 후진제거법 | 모든 변수에서 시작 → 하나씩 제거 |
| 단계적 선택법 | 전진 + 후진 혼합, AIC/BIC 기준 활용 |
📌 변수 선택의 기준: 정보 기준량
| 지표 | 설명 |
| AIC (Akaike Information Criterion) | 모델 적합도와 복잡도의 균형 고려 (낮을수록 좋음) |
| BIC (Bayesian Information Criterion) | AIC보다 패널티가 더 큼 (보수적 선택 기준) |
2. 로지스틱 회귀분석 (Logistic Regression)
2.1 기본 개념
- 적용 대상: 종속변수가 범주형(특히 이진): 성공/실패, 스팸/비스팸 등
- 예시
- 고객이 이탈할까(1) vs 유지할까(0)
- 이메일이 스팸일까(1) vs 아닐까(0)
2.2 개념 흐름
| 단계 | 설명 |
| 확률 (P) | 성공할 확률 |
| 오즈 (Odds) | 성공 확률 / 실패 확률 = P / |
| 로짓 (Logit) | 오즈에 로그 취한 것: log(P/1 - P) → 선형 회귀처럼 표현 가능 |
| 시그모이드 함수 | 로짓의 역함수 → 0~1 사이 확률로 변환하는 곡선 함 |
2.3 시그모이드 함수(Sigmoid)
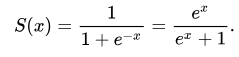
| x 값 | 확률값 p |
| 매우 작음 | p ≈ 0 |
| 0 근처 | p ≈ 0.5 |
| 매우 큼 | p ≈ 1 |
✅ X가 1 증가할 때, 확률은 e^β만큼 증가
(오즈 비율이 e^β배로 증가한다는 뜻)
✅ 해석
“고객의 연령이 1살 증가할 때, 구매할 확률은 1.5배 증가한다”
→ 이는 β≈l, 즉 오즈 비가 1.5라는 뜻
2.5 평가 지표
| 지표 | 설명 |
| Accuracy | 전체 중 정답 맞춘 비율 |
| Precision / Recall / F1 Score | 불균형 클래스 데이터에 더 적합 |
| ROC-AUC | 모델의 분류 성능을 곡선 아래 면적으로 평가 (1에 가까울수록 좋음) |
| Confusion Matrix | TP, FP, FN, TN으로 분류 결과 정리 |
3. 의사결정나무 (Decision Tree)
- 분류(Classification)와 회귀(Regression) 모두에 사용 가능한 분석 기법
- 데이터를 기준에 따라 트리 구조로 분할하여 의사결정을 내리는 방식
3.1 기본 개념
| 항목 | 설명 |
| 분석 목적 | 예측/분류/설명 등 다양한 목적으로 사용 |
| 출력 형태 | 트리(Tree) 구조 (노드 → 가지 → 리프) |
| 데이터 유형 | 정형 + 비정형(텍스트 등)도 일부 활용 가능 |
| 분류/회귀 모두 사용 가능 | |
- 분류: 예/아니오, 고객 등급 등
- 회귀: 주가 예측, 매출 예측 등
3.2 분할 기준
✅ 분류 트리
| 기준 | 설명 |
| 지니지수(Gini Index) | 노드 내 불순도 측정 (값이 작을수록 순수) |
| 엔트로피(Entropy) | 정보이득 최대화를 기준으로 분할 |
| 카이제곱 통계량 | 범주형 데이터에 강함, 통계적 유의성 기반 |
📌 지니지수 vs 엔트로피
- 둘 다 노드의 순수도를 평가
- 지니지수는 계산 간단, 엔트로피는 정보 이론 기반
✅ 회귀 트리
| 기준 | 설명 |
| MSE (Mean Squared Error) | 자식 노드의 제곱 오차 평균을 최소화하는 방향으로 분할 |
| MAE (Mean Absolute Error) | 절댓값 기준의 평균 오차를 최소화하는 방식 (MSE보다 이상값에 덜 민감) |
| 분산 감소 (Variance Reduction) | 분할 전 분산에서 분할 후 가중 평균 분산을 뺀 값이 최대가 되도록 |
3.3 과적합 방지 방법
| 기법 | 설명 |
| 정지규칙 (Stopping Rule) | 깊이가 일정 수준에 도달하면 더 이상 분할 X |
| 가지치기 (Pruning) | 학습 후 성능 개선을 위해 불필요한 가지 제거 |
| 사전 가지치기 | 분할 조건에 제한 (예: 최소 샘플 수 등) |
| 사후 가지치기 | 완성된 트리에서 성능 낮은 가지 제거 |
3.4 의사결정나무 알고리즘 구조
- 모든 데이터는 루트 노드에 존재
- 최적의 속성 기준으로 데이터 분할
- 각 분할된 그룹을 자식 노드로 생성
- 더 이상 분할이 불가능하거나 조건 만족 시 리프 노드
- 트리 완성 후 분류 or 예측에 사용
3.5 의사결정나무의 장점과 단점
| 장점 | 단점 |
| 구조가 직관적, 시각화 쉬움 | 과적합 발생 가능성 높음 |
| 전처리 간단 (스케일링 불필요) | 데이터 소량 시 불안정 |
| 결과 해석력 높음 | 분할 기준이 조금만 달라져도 트리 구조 크게 변화 |
4. 인공신경망 (Artificial Neural Network)
- 인공신경망은 인간의 뇌 신경 구조를 모방한 기계학습 알고리즘
- 복잡한 비선형 관계도 학습할 수 있는 강력한 예측 모델
4.1 기본 구조
| 계층 | 설명 |
| 입력층 (Input Layer) | 입력 데이터의 특징(Feature)들이 들어가는 시작점 |
| 은닉층 (Hidden Layer) | 입력을 처리하고 변형하는 중간 계층, 비선형성 부여 |
| 출력층 (Output Layer) | 최종 예측값을 출력 (예: 클래스 확률, 회귀값 등) |
📌 은닉층이 많아지면 → 딥러닝(Deep Learning)
4.2 활성화 함수 (Activation Function)
- 활성화 함수는 인공 신경망에서 입력 신호를 출력으로 변환하는 함수
- 뉴런이 얼마나 활성화되는지 결정
✅ 은닉층에서 사용되는 함수
| 함수 | 출력 범위 | 특징 |
| Sigmoid | (0, 1) | 확률처럼 해석 가능, gradient vanishing 문제 |
| Tanh | (-1, 1) | Sigmoid보다 중심성 우수 |
| ReLU | [0, ∞) | 빠른 수렴, 음수는 0으로 처리 |
| Leaky ReLU | 실수 전체 | 음수도 조금은 통과시킴 |
| ELU, GELU | 다양 | 최근 고급 모델에서 자주 사용되는 비선형 함수들 |
✅ 출력층에서 사용되는 함수
| 함수 | 용도 | 특징 |
| Sigmoid | 이진 분류 | 0~1 확률 출력 |
| Softmax | 다중 분류 | 각 클래스의 확률 총합 = 1 |
4.3 학습 흐름
- 순전파 (Forward Propagation)
→ 입력값이 계층을 따라 전달되어 예측값 계산 - 손실 계산 (Loss Function)
→ 예측값과 실제값 차이 계산- 회귀: MSE (Mean Squared Error)
- 분류: Cross-Entropy Loss
- 역전파 (Backpropagation)
→ 오차를 역으로 전달하며 가중치 갱신 방향 계산 - 경사하강법 (Gradient Descent)
→ 오차를 최소화하는 방향으로 가중치 조정
4.4 과적합 방지 기법
| 기법 | 설명 |
| Dropout | 학습 중 일부 뉴런을 무작위로 제거하여 과적합 방지 |
| L1/L2 정규화 | 가중치 크기에 패널티 부여 (L1: 라쏘, L2: 릿지) |
| Early Stopping | 검증 성능이 악화되면 학습 조기 종료 |
| Batch Normalization | 은닉층 출력을 정규화하여 학습 안정화 |
| 데이터 증강 | 입력 데이터를 다양화하여 일반화 성능 향상 (이미지, 텍스트 등) |
5. 서포트벡터머신 (SVM, Support Vector Machine)
- 데이터의 경계에 최대한 넓은 마진(Margin)을 갖는 초평면을 찾아
- 이진 분류 또는 회귀 문제를 해결하는 머신러닝 알고리즘
5.1 핵심 개념
| 개념 | 설명 |
| 초평면 (Hyperplane) | 두 클래스를 나누는 결정 경계 |
| 마진 (Margin) | 두 클래스에서 가장 가까운 데이터(서포트 벡터)와 초평면 사이 거리 |
| 최적화 목표 | 마진을 최대화하는 초평면을 찾는 것 |
| 서포트 벡터 | 초평면 경계에 가장 가까이 위치한 결정에 영향을 주는 데이터 포인트 |
📌 마진이 넓을수록 → 일반화 성능 향상
5.2 유형 (마진 설정 방식)
| 유형 | 설명 | 특징 |
| 하드 마진 SVM | 완벽한 분리를 가정, 오류 허용 안함 | 이상치에 민감함 |
| 소프트 마진 SVM | 오류 일부 허용, 일반화 성능 향상 | 실전에서 더 자주 사용 |
📌 소프트마진에서는 규제 파라미터 C로 오류 허용 범위 조절
→ C ↑ → 과적합 우려 / C ↓ → 과소적합 가능
5.3 커널 기법 (Kernel Trick)
- 비선형 데이터를 고차원 공간으로 매핑하여 선형 분리가 가능하게 만드는 방식
| 커널 종류 | 설명 | 활용 |
| 선형 커널 | 선형 분리 가능할 때 사용 | 고차원 희소 데이터 (텍스트) |
| 다항 커널 (Polynomial) | 곡선 경계 분리 | 복잡한 경계 |
| RBF (Radial Basis Function) | 가우시안 기반, 가장 많이 사용 | 이미지, 센서 등 |
| Sigmoid 커널 | 인공신경망 구조 유사 | 특수 목적에서 제한적 사용 |
📌 커널 기법은 실제 고차원으로 변환하지 않고 내적(inner product)으로 계산해 연산 효율 유지
5.4 SVM의 장점과 단점
| 장점 | 단점 |
| 마진 최대화로 일반화 성능 우수 | 대용량 데이터 처리 속도 느림 |
| 고차원에서도 잘 작동 | 커널, 하이퍼파라미터 튜닝 어려움 |
| 커널 기법으로 비선형 분류 가능 | 다중 클래스 분류에 한계 존재 (→ One-vs-Rest로 확장) |
6. 연관성 분석 (Association Analysis)
- 연관성 분석은 "어떤 항목이 함께 발생하는 패턴"을 찾아내는 분석 기법
- 대표적으로 장바구니 분석(Market Basket Analysis)이 있음.
6.1 개념 및 목적
- "A를 구매한 고객은 B도 구매할 확률이 높다"라는 형태의 조건 → 결과 규칙을 도출
✅ 활용 예시
- A: 우유 구매
- B: 빵 구매
→ “우유를 구매한 고객 중 80%는 빵도 구매했다”
6.2 핵심 지표
| 지표 | 수식 | 의미 |
| 지지도 (Support) | P(A∩B) | 전체 거래 중 A와 B가 동시에 발생한 비율 |
| 신뢰도 (Confidence) | P(A∩B)/P(A) | 품목 A를 구매했을 때, 품목 B를 추가로 구매할 확률 |
| 향상도 (Lift) | P(A∩B)/P(A)P(B) | 품목 A를 구매했을 때, 품목 B를 추가로 구매할 확률 |
✅ 향상도 해석
| 향상도 값 | 의미 |
| > 1 | A와 B는 양의 상관관계 (A를 구매했을 때 B를 구매할 가능성이 높다) |
| = 1 | A와 B는 무관 |
| < 1 | A와 B는 음의 상관관계 (A를 구매했을 때 B를 구매할 가능성이 낮다) |
6.3 대표 알고리즘
- Aporiori
- 최소 지지도 이상인 빈발 항목집합을 먼저 탐색
- 후보 항목 조합을 계속 생성 → 계산량 ↑
- 개선 알고리즘: Hash-based, Partition, DHP 등
- 후보 조합 없이 빈발 항목집합 탐색
- 트리 기반 구조 사용 (FP-Tree)
6.4 실전 예시
총 거래 수: 1,000건
우유(A): 300건
빵(B): 400건
우유 + 빵 함께 구매: 240건
| 지표 | 계산 | 결과 |
| 지지도 | 240 / 1000 | 0.24 |
| 신뢰도 | 240 / 300 | 0.80 |
| 향상도 | 0.80 / 0.40 = 2.0 | 강한 양의 연관관계! |
7. 군집분석 (Clustering
- 군집분석은 지도 학습 없이 유사한 데이터끼리 자동으로 그룹화(클러스터링)
- 비지도 학습(Unsupervised Learning) 기법
7.1 목적 및 핵심 개념
| 항목 | 설명 |
| 목적 | 유사한 특성을 가진 데이터들을 군집으로 나누어 숨겨진 패턴/구조 파악 |
| 활용 예시 | 고객 세분화, 이상치 탐지, 이미지 분류, 추천 시스템 등 |
7.2 거리 측도 (Distance Measures)
| 거리 측도 | 설명 |
| 유클리디안 거리 | 가장 일반적인 직선 거리 |
| 맨해튼 거리 | 축을 따라 이동한 총 거리 ( |
| 마할라노비스 거리 | 변수 간 상관관계를 고려하여 거리 계산 |
| 민코우스키 거리 | 유클리디안과 맨해튼 거리의 일반화 형태 |
📌범주형 데이터 유사도
| 측도 | 설명 |
| 자카드 유사도 | 교집합 / 합집합 → 집합이 겹치는 정도 |
| 코사인 유사도 | 두 벡터 간의 각도를 기반으로 유사도 측정 (0~1) |
| ※ | 1에 가까울수록 유사, 0이면 무관 |
7.3 계층적 군집 (Hierarchical Clustering)
| 항목 | 설명 |
| 방법 | 데이터 간 거리를 기준으로 계층적으로 병합 or 분할 |
| 결과 시각화 | 덴드로그램 (Dendrogram): 트리 형태 시각화 |
| 연결 기준 |
- 단일 연결법: 가장 가까운 거리
- 완전 연결법: 가장 먼 거리
- 평균 연결법: 평균 거리
- 중심 연결법: 중심 간 거리
- 와드 연결법: 분산 증가 최소화
7.4 K-평균 군집 (K-Means Clustering)
| 항목 | 설명 |
| 과정 | 1. K값 설정 2. 초기 중심점 설정 3. 각 데이터 → 가장 가까운 중심에 할당 4. 군집 평균으로 중심 재설정 5. 중심 이동이 없으면 종료 |
| 특징 | - 거리 기반 군집화 - 빠르고 계산 효율적 - 초기값에 민감 → 결과 불안정 가능성 |
| K 결정법 | - Elbow Method: SSE 감소량이 급격히 줄어드는 지점에서 최적 K 선택 - Silhouette Score: 군집의 응집도와 분리도를 종합적으로 평가 |
| K-Medoids (PAM) | - 평균이 아닌 실제 데이터 중 하나를 중심점으로 사용 - 노이즈에 강하고 극단값 영향 적음 |
7.5 기타 군집 기법
| 기법 | 특징 |
| DBSCAN (Density-Based Spatial Clustering of Applications with Noise) |
- 밀도 기반 클러스터링 - K값 미지정 - 이상치(노이즈) 감지에 탁월 - 밀도 기준 설정 필요 (ε, MinPts) |
| 퍼지 군집화 (Fuzzy C-Means) |
- 하나의 데이터가 여러 군집에 확률적으로 속함 - 군집 간 경계가 모호한 경우 유리 |
| EM 알고리즘 (Expectation Maximization) |
- 각 군집이 **확률 분포(예: 가우시안)**를 따른다는 가정 - E-step: 기대값 계산 - M-step: 최대 가능도 추정 |
| SOM (Self-Organizing Map) |
- 신경망 기반 군집화 + 차원축소 - 입력 데이터를 2차원 격자에 시각적으로 배치 - 유사한 데이터들이 가까운 노드로 맵핑됨 |
728x90
반응형
LIST